http://www.cnblogs.com/c-cloud/p/3224788.html

 

 例如： 当上面的长串遍历到C时，与子串未匹配上失败，如果从头再来则上面子串是从B开始，子串从A开始；效率实在太低。

          由图可知，前面已经有6个元素完全匹配上；而这6个元素本身的  部分匹配值位2，也就是从左往右；从右往左共同的子串，长度为2。既然6个元素+C无法与子串匹配上；

那么退而求其次，(长串中)是否右边小子串(公共串)+C,与子串从左往右公共串+1的元素匹配上呢？那么也就是，子串从C的位置开始，长串匹配位置不动，有效提高了速度。继续下去，就找到了长串。

 

 

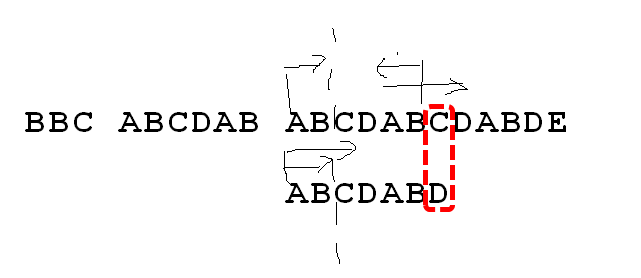
 部分匹配表

q = 1;

q = 2;

q = 3;

......

 

 

 

　　

 

#include
     
      #include
      
       void makeNext(const char P[],int next[]){//找到P数组的部分匹配表。    int q,k;    int m = strlen(P);//字符串长度    next[0] = 0;//第一个元素    for (q = 1,k = 0; q < m; ++q)//k从左往右0开始，同时它的移动表示成功匹配上的长度     q是确定长度，从1开始最大到m-1，匹配时，从右往左    {        while(k > 0 && P[q] != P[k])//当存在公共子串，或者说是部分匹配值时，             k = next[k-1];//不匹配时，最原始的做法就是，k又从0开始，q确定还是q不变从右往左，求解出next[q]
      
     

//此处，子串不从0开始，而是从next[k-1]继续与q进行匹配，依次递推，压缩空间去搜索。

// 充分利用子串前缀和后缀的对称性，加快搜索速度        if (P[q] == P[k])//当匹配上时，则k移动一步        {            k++;//匹配上的长度        }        next[q] = k;//记录部分匹配值    }}int kmp(const char T[],const char P[],int next[]){    int n,m;    int i,q;    n = strlen(T);    m = strlen(P);    makeNext(P,next);    for (i = 0,q = 0; i < n; ++i)//长串q移动一位    {        while(q > 0 && P[q] != T[i])//长串q位置不动            q = next[q-1];//当不等时，匹配子串P从next[q-1]开始匹配  i不变        if (P[q] == T[i])//当相等时，子串移动一位        {            q++;        }        if (q == m)//标识已经匹配到子串最后一个子串        {//返回长串中的子串起始位置， i-m+1            printf("Pattern occurs with shift:%d\n",(i-m+1));        }    }    }int main(){    int i;    int next[20]={0};    char T[] = "ababxbababcadfdsss";    char P[] = "abcdabd";    printf("%s\n",T);    printf("%s\n",P );    // makeNext(P,next);    kmp(T,P,next);    for (i = 0; i < strlen(P); ++i)    {        printf("%d ",next[i]);    }    printf("\n");    return 0;}